Binary
Example Codes:
Comparison: SAS #1
Comparison: R #1
Comparison: SAS #2
Comparison: R #2
Prediction: SAS #1
Prediction: R #1
Prediction: SAS #2
Prediction: R #2
Objectives
If your response variable is binary and you want to
analyze the relationship between the binary variable and other variables,
logistic regression can deal with that.
Assume the binary variable, y, only contains two values; 0 and 1.
Here is the logistic regression’s expression:

So, the outcome of logistic regression is the probability of getting the
response variable equal to 1.
The  is the odds ratio.
is the odds ratio.
General Example Code in SAS
PROC LOGISTIC DATA=SAS-data-set ;
CLASS variables ;
MODEL response=predictors
;
UNITS independent1=list;
ODDSRATIO <‘label’> variable ;
OUTPUT OUT=SAS-data-set keyword=name ;
RUN;
CLASS names the classification variables to be used in
the analysis. The CLASS statement must precede the MODEL statement. By default,
these variables will be analyzed using effects coding parameterization. This
can be changed with the PARAM= option.
MODEL specifies the response variable and the
predictor variables.
OUTPUT creates an output data set containing all the
variables from the input data set and any requested statistics.
UNITS enables you to obtain an odds ratio estimate for
a specified change in a predictor variable. The unit of change can be a number,
standard deviation (SD), or a number times the standard deviation (for example,
2*SD).
ODDSRATIO produces odds ratios for variables even when
the variables are involved in interactions with other covariates, and for
classification variables that use any parameterization. You can specify several
ODDSRATIO statements.
Outputs
The Model Information table describes the data set,
the response variable, the number of response levels, the type of model, the
algorithm used to obtain the parameter estimates, and the number of observations
read and used.

The Number of Observations Used is the count of all
observations that are nonmissing for all variables
specified in the MODEL statement. The ages of 263 of these 1309 passengers
cannot be determined and cannot be used to estimate the model.

The Response Profile table shows the response variable
values listed according to their ordered values. By default, PROC LOGISTIC
orders the response variable alphanumerically so that it bases the logistic
regression model on the probability of the smallest value. Because you used the
EVENT=option in this example, the model is based on the probability of
surviving (Survived=1). The Response Profile table also shows frequencies of
response values.


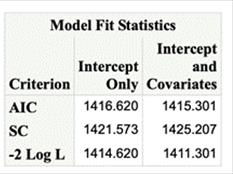
The Model Fit Statistics provides three tests
1. AIC is Akaike’s ‘A’ information criterion.
2. SC is the Schwarz
criterion.
3. -2 Log L is -2 times the
natural log of the likelihood.
-2 Log L, AIC, and SC are goodness-of-fit measures
that you can use to compare one model to another. These statistics measure
relative fit among models, but they do not measure absolute fit of any single
model. Smaller values for all of these measures
indicate a better fit.
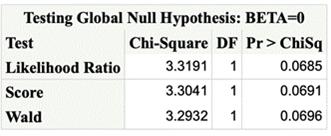
The Testing Global Null Hypothesis: BETA=0 table
provides three statistics to test the null hypothesis that all regression
coefficients of the model are 0.
The Analysis of Maximum Likelihood Estimates table
lists the estimated model parameters, their standard errors, Wald Chi-Square
values, and p-values.
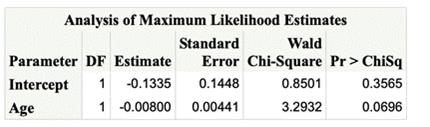
This information can be expressed in the below equation:

The Wald chi-square and its associated p-value test whether
the parameter estimate is significantly different from 0. For this example, the
p-values for the variable Age are not significant at the 0.05 significance
level (p=0.0696). It cannot be concluded that Age is not important in a
multivariate model. The
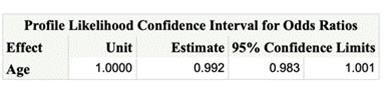
odds ratio and confidence interval can be found in the following table: